大话数据结构
第一章 绪论
数据项是最小单位，组成数据元素。一般只讨论数据元素。
数据结构：相互之间存在一种或多种特定关系的数据元素的集合
逻辑结构：
集合。各个元素平等。
线性：一对一
树：一对多
图：多对多
物理结构：逻辑结构的储存形式
顺序存储：如数组
链式存储：如链表，指向下一个元素的地址
数据类型：不同类型分配不同内存
原子类型：不可再分，整型、字符型等
结构类型：原子类型组合而成
第二章 算法
算法：解决特定问题求解步骤的描述。指令的有限序列。
好的算法：
正确：合法输入有正确输出，边界条件也能正确
可读
健壮：不合法输入也能做出处理
效率高：时间、空间
计算成本：
计算对运行时间有消耗的基本操作执行次数
时间复杂度
常数阶：O(1)
分支结构
线性阶：O(n)
循环n次，里面是O1操作
对数: O(logn)
每次循环，都离结束更近
平方阶：O(n2)
嵌套，On套On。包括外面i，里面从i开始，也是On2
空间复杂度
原地：O(1)
第三章 线性表
数组。
排队，有顺序。一对一。
存取时间O(1)。删除增加，O(n)
链表
存取O(n)，插入O(1)
删除表：留两个变量p和q，p获取当前节点，q获取p指向的节点，然后释放p。q给p，以此往复
静态链表
给没有指针的语言，来描述单链表。用数组代替指针。
数组每个下标对应两个：数据data，next指针的cur
有删改的时候，直接放在后面，然后用cur指向新增的地方
循环链表
用尾指针来表示循环链表
这样查找尾节点只用O(1)，头节点是rear.next.next，也是O(1)
双向链表
多写一个指针记录上一个节点。
第四章 栈与队列
顺序存储结构
下标为0的一端作为栈底。
定义top变量存栈顶元素位置。空栈的top为-1。
需要事先确定数组的存储大小。
两栈共享空间
很可以一个栈快满，另一个栈还空。
只要top1和top2不见面，两个栈就能一直使用
适合一个栈增长，另一个栈减少的情况。
栈的链式存储（链栈）
除非内存满，不然栈不会满
进栈和出栈都是O(1)
如果元素大小变化不可预料，用链栈。不然用顺序栈
栈的应用
实现递归
括号
遇到左括号就入栈，遇到右括号就出栈。期间算出其中内容。
乘除、加减
逆波兰，通过规则变成后缀表达式。
遇到数字输出，
如果是符号，且比栈顶符号优先级更高，就入栈。
如栈顶为+，输入*，则入栈
如果是比栈顶优先级低，那么全部清空。
如栈顶*，输入+，就清空栈输出，并把+入栈
如果是（，那么入栈，等待遇到），然后把其中包裹的内容都输出
遇到数字进栈，遇到符号，把栈顶两个数字出栈，运算，再塞回去。
队列
先进先出的排队。允许插入的叫队尾，允许删除的叫队头
循环队列
出栈后不一定要全部移动，只需要移动头指针即可
这样的话为了不溢出，就需要也移动尾指针。
当rear == front的时候，就会无法判断队列是否为空
设定一个标志位flag，来判断是否为空
必须保留一个位置，不能让
rear=front的情况发生
队列的链式存储结构
链表队列。比循环队列更灵活
第五章 string
根据字符串的编码，来比较字符串的大小。如查字典的过程。
顺序存储
一般把字符串长度保存在0下标的位置，或结尾的位置。
一旦有对字符串有预定义的大小，那么每次对字符串进行操作，就有可能溢出
链式存储
一个节点存放一个或多个字符。没被占满的，用#补全
总的来说不如顺序存储
模式匹配算法
子串的定位操作，就叫模式匹配
双循环，一个个字符比对
太低效
（外循环可以到内循环长度就停下，这样可以少跑内循环的距离）
kmp
双循环对于一些已经匹配过的字符串，还会再匹配一遍，kmp都省略掉了。
如果已知a与后面的b到e都不相同，且一开始a到e都是匹配的。
比如abcdefgab里面找abcdex
因此可以直接跳过外循环的b到e。换言之，外循环的i不变小。内循环跑到1
如果后面有重复
如abcabcabc里找abcabx
那么内循环的j就跑到3，因为第二轮的时候，ab已经比较过了。
第六章 树
根节点唯一，子节点互不相交。即子节点不能互连，只能从上到下。
度degree：节点有多少子节点。
叶节点度为0。整个树的度，就是节点中最大的度。
层次level
最大层称为深度或高度
有序/无序
如果从左至右不能互换，就是有序
森林
多棵互不相交的树的集合。
存储结构
因为可以一对多，因此无法用物理存储位置反映逻辑关系。
双亲表示法
每个节点一定有双亲。因此每个节点要存一下双亲在哪。
如果有从根到叶的需要，可以再存一下第一个左节点的指针
如果有表示兄弟关系的需要，可以再存一下右兄弟的指针
孩子表示法
兄弟节点之间，是用顺序存储，用链表指向子节点。
因此每个节点都存有数据和指针两组数据。
也可以再加一个指针，指向自己的双亲
孩子兄弟表示法
一个指针指子节点，一个指针指右边第一个兄弟节点
这就把一个复杂的树变成一颗二叉树
二叉树
左右子树有顺序，从小到大。
满二叉树：全部塞满
完全二叉树：横着标数字，不能有缺
存储结构
数组
只有是完全二叉树，才可以放在数组当中。
其他的不行。不然右斜树就太浪费空间了。
链表
二叉链表，数据+左指针+右指针
遍历
前序：从上到下，先左，深度优先
中序：从下到上，左到右。【相当于竖着从左到右的遍历】
后序：先按掉根不管，一根根分支遍历。先下后上，先左后右，最后到根。
层序：左到右，广度优先
线索二叉树
二叉树有很多空指针，尤其叶子比较多的时候。
用空指针记录前驱和后继的节点。【或者说是二叉树上左边和右边的节点】
指向的指针叫线索。
相当于变成一个双向链表。
不过这需要增加一个标志位，来表明是指上面还是下面。
【为啥感觉空间反而用的更多了。。。用空间换遍历的速度吗】
用二叉树表示树、森林
树 =》 二叉树
二叉树 =》树
二叉树 =》森林
霍夫曼树、霍夫曼编码
把学生成绩归入优良中差。
如果是从优到差一步步判断，可能效果不是很好，因为多数人集中在“中”和“良”。这就需要多次判断才能达到。
带权路径长度
从根节点到目标节点经过的节点数（路径长度）
走到这个节点的概率/所占比例
加权和就是WPL
构造霍夫曼树方法
目标是树两边概率要接近。以此来减少判断的次数。
方法是，概率从小到大排列。取概率最低的组成一颗小的左右子树，然后把总概率作为节点，放进概率排列中。
以此类推，最终得出整棵树
霍夫曼编码
字母、汉字出现的频率是不同的。
高频字符应该用更短的编码，低频字符用更长的编码，以此来节约总编码长度。
假设一共有这些数字，然后根据频率构成霍夫曼树：
左0右1，得到每个字符的编码。
完成编码和解码需要两个条件：
任何字符的编码，不能是另一个字符编码的前缀。 如1001和10会混淆。
双方要用同一套霍夫曼树 解码的时候就顺着根节点去找，找到了就输出字符，然后顺着编码继续从根节点找
比如100101，解码就是ba
第七章 图
图的顶点不能为空。任意两个顶点的逻辑关系，用 边 来表示
图的存储结构
邻接矩阵
顶点用一维数组。边或弧用二维数组来存，即一个矩阵。
无向图的边数组是一个对称矩阵
邻接表
如果边少，那么用这个就有点浪费
用数组和链表相结合的方法
这记录的都是从节点出去的弧。也可以专门建立一个表，放节点进去的弧
正反结合起来就是十字链表
图的遍历
深度优先
就是树的前序遍历
广度优先
最小生成树
构造联通网的最小代价生成的树
prim普里姆算法：
某个顶点为起点，逐步找各个顶点最小成本的边来构建最小生成树。【有点像贪心算法】
最短路径
两顶点之间经过的边上权值之和最少的路径
迪杰斯特拉Dijkstra算法
一步步求出到各个顶点之间最短路径
弗洛伊德Floyd算法
先有一个直接跑过去的矩阵。如果从a到b绕一下的成本更小，就把成本更小的路径替换掉原来的路径。
感觉就是一个迭代的过程
拓扑排序
有一堆任务，互相有关联，如何选择先做啥后做啥呢？
拓扑排序，就是把这个坍缩成一个有先后顺序的链表，然后一个个跟着做就行了。
把没依赖的push进栈
pop栈，把pop出的内容变成孤儿。需要它的节点变成不需要它
然后重新看谁没依赖，再push进去，以此往复
关键路径
一堆任务有优先级，有依赖。怎么看最长需要时间。
感觉类似于求最短路径，不过是变成求最长
第八章 查找
静态查找：就在表里面找
动态查找：找不到做点动作，比如找不到就插入；或者查到删除
顺序表查找
排列整齐，构成线性表，进行查找。
顺序查找
就从头到尾一个个匹配
优化方法，是把a[0]设置为要找的key，然后从后往前找
这样一次匹配就行了，不用每次i都要和n匹配一下
也可以把常用的放在前面，提高查找的效率。
有序表查找
先做好排列，比如根据拼音顺序排列，这样找起来方便
二分查找，就很快。
插值查找，就根据要找的东西靠近哪里，就先在哪里找起来。比如a打头的就在前面找。
根据查找关键字，与表中最大最小记录关键字比较后查找。
中间那个是插值计算公式
斐波纳切查找
计算更加简单，大部分情况比二分要好。
索引
数据结构目的是提高数据的处理速度。
索引，把关键字与他对应的记录相关联的过程。
比如用小本子记下重要的东西放在了哪里。需要用的时候看这个小本子就行了。
线性索引、树形索引、多级索引
线性就是把索引项集合成一个线性的索引表。
线性索引可分：稠密索引、分块索引、倒排索引
稠密索引
数据的每个记录都对应一个索引项
索引要根据关键码有序排列
【就是目录咯。。】
分块索引
图书馆的藏书。分块放。每一块再建立一个索引项。
块间有序，块内无序。
换言之只用排序块与块之间。块内就不用管，节约一下排序的成本。
每块的索引：
存最大值
块个数
首个元素的地址
【感觉就是分解了一下查找的任务。。】
倒排索引
比如搜索引擎搜索。
维护一个有序的单词表。找的时候就直接找这个单词表，再跳转到对应的网址
优点是查找非常快，但维护起来很麻烦。尤其多个网站都有同一个关键字
优化方法：
文章编号可以用增量，记录差值
关键字也可以记录差值
一次搜索只展示其中的10条
二叉排序树
插入和查找同样高效
左边节点都小，右边节点都大
平衡二叉树
左子树和右子树高度差最多为1
最小不平衡子树
从这个节点开始不平衡了。
原理
插入时，先检查会不会破坏平衡，如果是，就找到最小不平衡子树，对其进行旋转等操作，使其平衡。
这个数字是bf值，就是衡量左右子树的差距。
bf=1就右旋，bf=-1就左旋。这需要从下往上转。
旋转后要重新排列3这个节点
多路查找树(B树)
如果硬盘和内存差距很大，那么访问时间不仅仅是查找元素的时间，还要考虑 访问时间 和 会有多少次单独访问。
因此要降低对外存设备的访问次数。也就是让树越扁越好，因此一次就读区一层。
一个节点只存一个元素，或只有两个子树。数据量大的时候就需要多次读取外存。
多路查找树，每个节点子树可以有多个，每个节点也能存多个元素
其中四种：2-3树、2-3-4树、B树、B+树
2-3树
每个节点可以有一个2节点的孩子，也可以有一个3节点的孩子。
2节点，一个元素+0或2个孩子。很像二叉树，但要么没孩子，要么有两个。
3节点，两个元素和三个孩子。也是0或3个孩子。左到右，小中大
【换言之就是把每个节点扩容，最多可以放两个元素】
2-3树插入和删除
2节点插一个变3节点
3节点插一个，要把整个相关的树都打乱重排
删一个也要重排
2-3-4树
扩展2-3树，一个节点最多放三个元素和四个孩子
也是插入和删除会导致结构重排
B树
2-3树和2-3-4树都是B树的特例
节点最大的孩子树，是B树的阶。3阶、4阶B树
比如根节点1001阶有1000个元素，可以存10亿元素。因此只需把根节点留在内存，只需要最多读两次硬盘就能获取某个关键字。
即每次磁盘访问都要获得最大数据量。
B+树
B树遍历比较麻烦，需要在子树和根节点中来回跳。
根节点元素会在子树中最后重新出现
子树前面会指向后面
分支节点只是索引，不存特定内容。顺序查找就直接从左往右查即可。
更适合有范围的查找。
散列表/哈希表查找
不用比较下标大小，直接通过关键字来查找记录内存的存储位置。
散列技术：存储位置和关键字之间建立一个对应关系。换言之，输入关键字，就能输出对应存储位置。
函数叫 散列函数/哈希函数。连续存储空间叫 散列表或哈希表。
存储地址都是用哈希函数算出来的。
【感觉类似于用哈希函数编码和解码】
适合一一对应的精确查找。
不适合范围查找、结果多条等查找。
散列函数的构造
希望这个函数：计算简单、冲突少。地址分布均匀。
根据关键字规律
抽取关键字差异
平方取中间三位。适合不知道分布，且位数不大的情况
三位一组，加起来取后三位
求余数
随机数
处理冲突
有冲突就再找地址。
线性
平方运算
随机数
准备多个散列函数，一个不行换一个
不换地方，有冲突就增加链表长度
专门找个地方放冲突的数
第九章 排序
稳定性：如果两个值相等，那么排序前在前的，排序后也要再前面
内排序：排序过程中，全部记录放在内存中；
外排序：需要放一点东西在外存，排序时还要交换数据
内排序：插入、交换、选择、归并
冒泡排序
拿着一个数，遇到比它大的就交换位置，就从下往上不断冒泡就完事了。
但如果只需要排序前几个，那么之后的对比判断就是多余的。可以加一个flag，如果没有交换，就停止排序。
简单选择排序
对每个位置，找到后面的最小值，与当前值进行交换。
直接插入排序
将记录插入到已经排序好的有序表中
希尔排序
先分组排序，让总体来看小的在前，大的在后，然后再插入排序。
大意就是，先粗排，再精排。
需要定一个增量，一开始很大，把两端两个值排序。然后这个增量慢慢缩小为1
堆排序
之前排序，遍历的结果没有保存，因此有重复的劳动。
可以在一次排序过程中，对其他记录做出相应调整，就比较高效。
堆：完全二叉树，每个节点值都大于或小于左右孩子。大于叫大顶堆；小于叫小顶堆
将待排序的序列构造成一个大顶堆
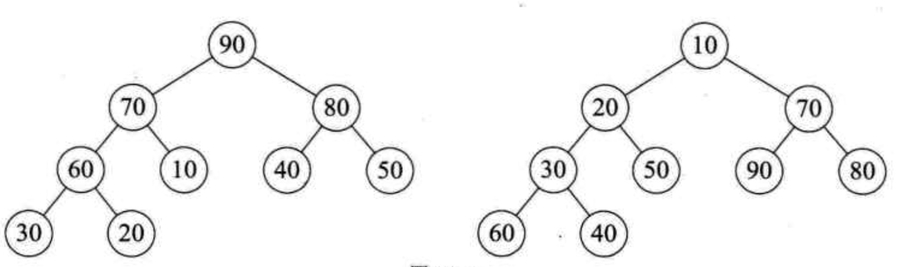
根节点即最大值，拿掉。也就是和末尾元素互换。
即把最大值放在序列尾
重新排序堆
完全二叉树性质：
以此来确定子树位置
归并排序
两两排序后再合并排序
快速排序
一次排序把序列分成两部分，一部分全部小于另一部分。再分别进行排序。
每一轮都拿着一个数，叫枢轴，然后排序数组。令其左边的数都比他小，右边都比他大。
方法是双指针，如果左边比右边的大，就交换双方位置
优化：
总是选取第一个数作为枢轴排序，是不合理的。
我们是希望枢轴是在中间的位置。如果选择的数太小或太大，就没有再拆分的意义了。
随机选数
选三个数先排序，然后取中间数。一般选左中右，无序的数组不需要再随机选。
如果序列非常大，可以选9个数。分三次每次取三个数，三个中数再取中数。
优化交换
枢轴备份。交换的过程就写入，而不是真的去交换。low=high的时候再写入
小数组还是用直接插入最好。
尾递归优化
Last updated
Was this helpful?
